Diferentes maneras de contar

¿Cuántos sudokus hay? ¿Cuántas maneras hay de colorear los países de un mapa mundi? ¿Cómo organizar un festival de cine?

Izquierda: un mapa de Alemania (izquierda) y un sudoku (derecha) y sus representaciones en forma de grafos. Foto: Max Planck Institute for Dynamics and Self-Organization.

Antes de espantar a los posibles lectores de este artículo al mencionar la palabra “Matemáticas” recordemos que hay ramas de las Matemáticas, como la Matemática Discreta, que tienen aplicaciones directas en la vida cotidiana, constituyendo también parte de las bases de las ciencias de la computación.
¿Como podemos organizar el horario de proyección de las películas de un festival de cine de tal modo que aquellos interesados en distintos tipo de películas puedan asistir a todas ellas sin que las películas dentro del mismo tipo no se solapen? ¿Cuántos sudokus hay? ¿Cuántas maneras hay de colorear los países de mapa mundi? Vamos a ver que la Teoría de grafos trata de contestar a estas preguntas.
Muchos de estos problemas se pueden representar mediante un grafo. Un grafo se puede dibujar como una serie de puntos, denominados vértices, unidos por líneas llamadas aristas. La forma del grafo no es importante, así como la longitud de las aristas, aunque se puede asociar un peso a cada una de ellas. En los programas informáticos los grafos se representan mediante matrices, de esta manera es mucho más fácil su manipulación y más sencillo el efectuar operaciones sobre ellos.
A diferencia de la mayoría de teoremas clásicos de las Matemáticas, muchos de los algoritmos que resuelven de manera eficiente problemas implementados sobre grafos se descubrieron hace relativamente poco tiempo, en el pasado siglo. Así tenemos el algoritmos de Dijkstra (de 1959) que permite, por ejemplo, calcular el camino más corto entre dos ciudades sobre un mapa de carreteras, o el de Kruskal (de 1957) que permite, por ejemplo, saber el trazado de líneas telefónicas que interconecten distintos usuarios al menor costo gracias a que halla el árbol recubridor de peso mínimo.
Hay otros problemas más clásicos, como el de los puentes de Königsberg, ya analizado por Euler, que tuvieron solución hace tiempo gracias al algoritmo de Fleury. Este algoritmo nos permite, cuando es posible, resolver los típicos problemas de trazar un dibujo sin levantar el lápiz de papel y sin pasar más de una vez por el mismo sitio.
Pero hay otros problemas como el del viajante (que consiste en salir de la sede de la empresa y volver a ella visitando todas las ciudades una sola vez con el menor camino posible) que básicamente para el cual no hay un algoritmo que lo resuelva de manera eficiente. Aquí se entiende por “eficiente” el que sea resoluble en un tiempo polinómico. Es decir, que el tiempo de resolución en relación al tamaño del problema (en nuestro caso al número de vértices de nuestro grafo) crezca polinómicamente y no exponencialmente. Aunque hay muchos algoritmos que encuentran una buena aproximación al problema del viajante no existe ninguno que sea eficiente y que a la vez dé la mejor solución posible. La única manera de encontrar la mejor solución consiste básicamente en enumerar todas las posibilidades y escoger la mejor, algo sumamente ineficiente. Se sospecha que algunos de estos problemas nunca tendrán una solución eficiente (problemas NP y NP completos).
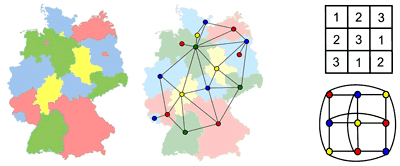
Los problemas relativos a la organización de horarios en festivales de cine, a posibles sudokus o a mapas del mundo se pueden intentar representar por grafos que tiene los vértices coloreados. En cada caso o problema los “colores” representan o simbolizan algo distinto y no necesariamente son literalmente colores.
En el ejemplo del mapa podemos asociar cada país a un vértice de un grafo y unirlos con una arista si tienen frontera en común. Dentro de las posibles coloraciones, las coloraciones propias son las más interesantes y consisten en que los vértices unidos por una arista no tengan el mismo color. En nuestro ejemplo pintar dos países vecinos con el mismo color no es una buena idea si los queremos distinguir en el mapa.
Saber cuantas coloraciones propias distintas con “q” colores se pueden obtener o el mínimo número de colores (número cromático) para colorear propiamente un grafo son preguntas muy difíciles de contestar. Contar cosas puede ser tremendamente difícil si el problema combinatorio no es muy sencillo.

Dos de las posibles 1152 maneras de colorear propiamente con cuatro colores un grafo en concreto. Foto: Max Planck Institute for Dynamics and Self-Organization.

Se conoce un algoritmo eficiente (de tipo voraz) que colorea propiamente un grafo para una ordenación de vértices dada. Si probamos con todas las ordenaciones y escogemos la que emplea el menor número de colores podemos averiguar el número cromático. Suena sencillo, pero es muy costoso al crecer factorialmente con el número de vértices. Si, por ejemplo, tenemos un grafo de sólo 10 vértices tendremos:

10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3628800 posibles ordenaciones.

Si tenemos uno de 100 vértices entonces tendremos:

100! = 9.332621544394418 × 10¹⁵⁷ ¡posibles ordenaciones!

A veces si el grafo no es uno general, sino un grafo más sencillo, como en el caso del que representa los países de un mapa (grafo planar) se puede hacer algo, incluso demostrar teoremas. Uno muy famoso dice que dado cualquier mapa geográfico, éste puede ser coloreado con cuatro colores diferentes, de forma que no queden regiones adyacentes con el mismo color. La demostración, que se fue asistida por computación, se realizó hace relativamente escasos años. Necesitaron más de 1200 horas de CPU para realizarla.
Aunque parezcan problemas académicos no lo son tanto y muchos campos de la Física y de otras ciencias se pueden aprovechar de cualquier avance en este campo.
Recientemente un grupo del Max Planck ha desarrollado un nuevo método de cálculo que permite resolver algunos problemas de coloreado de grafos de manera eficiente. El resultado no es muy importante, pero nos sirve para hablar de este tipo de problemas matemáticos y computacionales.
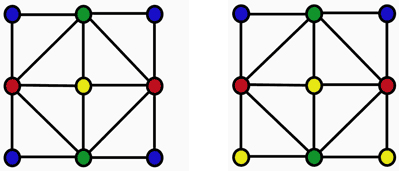
En todo caso su método permite responder a diversos problemas de coloreado de grafos de una manera más eficiente que hasta ahora. Se aplicaría a grafos en forma de red (por su similitud a una red cristalina) y se basa en dividir el problema en pequeños trozos. Trata de responder a la primera pregunta difícil de coloración propia antes mencionada sobre número de coloraciones. Dado un número determinado de colores, ¿de cuantas maneras podemos colorear un mapa? ¿Cuántos sudokus son posibles?
Una red, al ser un grafo sencillo, puede ser más fácil de estudiar, pero con la ventaja de poder aplicar los resultados a sistemas físicos, como una red cristalina con spines asociados a cada vértice o nodo de la red.
Frank van Bussel del MPIDS dice que “en los actuales algoritmos se tiene copia de toda la red para cada estado del cálculo y sólo cambios de un aspecto cada vez”. Al aumentar el número de vértices aumenta mucho el tiempo de cálculo. Para una red cuadrada del tamaño a la del tablero de ajedrez el tiempo de cálculo se estima en miles de millones de años. Con el nuevo algoritmo este mismo problema se puede calcular en siete segundos.
Con el nuevo método se explora vértice a vértice el sistema de tal modo que se efectúa el cálculo considerando sólo el próximo vértice y no la red completa. En cada paso, en lugar de evaluar el color a asignar, que implicaría saber las conexiones con los otros vértices, se evalúa una fórmula con ciertas incertidumbres. Según se progresa a lo largo de la red, barriendo todos los vértices, todas las conexiones se van poniendo de manifiesto y las incertidumbres finalmente desaparecen.
El método se puede aplicar además a sistema complejos sobre los que otros métodos son muy ineficientes, como en el caso de los sólidos antiferromagnéticos (en los que los spines tienden a orientarse antiparalelamente), permitiendo caracterizarlos desde el punto de vista termodinámico de esos sistemas físicos.
Partimos de la organización de festivales de cine, pasamos por mapas o sudokus y al final terminamos en el magnetismo que determina el funcionamiento del disco de ordenador que ahora está usando. No está mal para ser simples Matemáticas.